در مطلب گذشته در مورد مغناطیس صحبت شد. در این آموزش، به بررسی «اثر هال» (Hall Effect) میپردازیم.
فرض کنیم یک هادی الکتریکی مستطیلی داریم که جریان الکتریکی از آن عبور میکند. حال اگر یک میدان مغناطیسی به این هادی الکتریکی اعمال کنیم، در دو طرف هادی، اختلاف ولتاژ به وجود میآید.
این اختلاف ولتاژ که قابل اندازهگیری نیز هست، اثر هال نام دارد. «ضریب هال» (The Hall Coefficient) حاصل تقسیم میدان الکتریکی القایی به حاصل ضرب چگالی جریان و میدان مغناطیسی اعمال شده است. مقدار این ضریب به نوع، تعداد و خواص حاملهای بار بستگی دارد. حامل بار، واحد تشکیل دهنده جریان است. هادی، با استفاده از این مشخصه ماده تعریف میشود.
کشف
اثر هال در سال ۱۸۷۹ توسط «ادوین هال» (Edwin Hall) هنگامی که روی رساله دکترای خود در دانشگاه جانز هاپکینز کار میکرد، کشف شد. ۱۸ سال پیش از آنکه الکترون کشف شود، ادوین هال در اندازهگیریهای خود، پی به اثرات کوچکی برد. او، این اثرات کوچک را در مقاله «اثرات آهنربا بر جریان الکتریکی» منتشر کرد.
در واقع هال در آزمایشهای خود، دریافت که در فلزات، علامت حاملهای بار، منفی است. یعنی در فلزات، الکترونها حامل بار هستند. در آن زمان، پی بردن به ماهیت ماده یک شاهکار تجربی محسوب میشد.
تئوری
وقتی میدان مغناطیسی داریم، به این حاملهای بار نیرویی وارد میشود که به نام «نیروی لورنتس» (Lorentz Force) میشناسیم. وقتی میدان مغناطیسی وجود ندارد، حاملهای بار، تقریبا در خط مستقیم حرکت میکنند. اگر میدان مغناطیسی به صورت عمودی بر محور هادی مستطیل شکل اعمال شود، مسیر حرکت این حاملهای بار منحرف میشود. این انحراف، باعث جمع شدن بارهای مثبت در یک طرف هادی مستطیلی و بارهای منفی در طرف دیگر هادی میشود. پس، بارهای برابر ولی با علامت مخالف، در دو طرف هادی جمع میشوند. در نتیجه، یک توزیع نامتقارن از چگالی بار در طول «المان هال» به وجود میآید که جهت آن عمود بر جریان گذرنده از هادی و میدان مغناطیسی است.
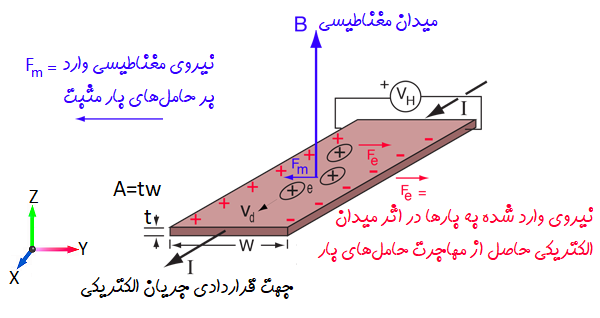
این توزیع نامتقارن حاملهای بار، یک میدان الکتریکی تولید میکند. میدان الکتریکی ایجاد شده، با ادامه مهاجرت حاملهای بار، مخالفت میکند. بنابراین تا زمانی که جریان از هادی عبور کند، یک اختلاف پتانسیل ثابت دو طرف هادی وجود خواهد داشت.
در الکترومغناطیس کلاسیک، الکترونها در خلاف جهت جریان I حرکت میکنند. (به طور قراردادی، جهت حرکت حفرهها همان جهت جریان I است. در فیزیک پایه بیان شده است که حفرهها حرکت نمیکنند)، اما در بعضی نیمههادیها، در حقیقت حفرهها با بار مثبت، حرکت میکنند.
برای یک فلز ساده، تنها یک نوع حامل بار داریم (الکترون). اختلاف ولتاژی که در دو سر هادی به وجود میآید ولتاژ هال () نام دارد. این ولتاژ را میتوان با استفاده از نیروی لورنتس محاسبه کرد.
در شرایط حالت دائم، بارها در جهت محور y حرکت نمیکنند. بنابراین نیروی مغناطیسی و الکتریکی وارد بر الکترونها در جهت محور y یکدیگر را خنثی میکنند. حالت دائم، به این معنی است که وقتی میدان مغناطیسی اعمالی و جریان الکتریکی عبوری در طول زمان ثابت باشند، همچنان اختلاف ولتاژ در دو طرف هادی مشاهده میشود و این میدانها یکدیگر را خنثی میکنند.
تعریف ولتاژ هال
اگر را سرعت سوق الکترونها بنامیم، با استفاده از قانون دست راست، عبارت در جهت منفی y است. نیروی وارد بر الکترونها به صورت زیر است:
$$F=q(E+v \times B)$$
در شرایط حالت دائم، نیروی الکتریکی و مغناطیسی وارد بر حاملهای بار با هم برابر میشوند، پس است. در نتیجه داریم:
$$E_y-v_x B_z = 0$$
که در آن ، میدان الکتریکی در جهت محور y است. این میدان، جهت انحراف الکترونها را نشان میدهد.
در سیم، به جای حفره، الکترون حرکت میکند. بنابراین:
$$q \rightarrow -q$$
و
$$q \rightarrow -q$$
بنابراین:
$$E_y=-\frac{V_H}{w}$$
با قرار دادن این تغییرات داریم:
$$V_H=v_x B_z w$$
جهت حرکت حفرهها طبق قرارداد، خلاف جهت حرکت الکترونها است. بار حفره نیز طبق قرارداد، مثبت است. با استفاده از رابطه سرعت سوق و جریان در هادی، داریم:
از اثر هال میتوان برای اندازهگیری چگالی جریان یا میدان مغناطیسی استفاده کرد.
یکی از ویژگیهای مهم اثر هال، این است که بین بارهای مثبت عبوری در یک جهت و بارهای منفی عبوری در خلاف جهت تفاوت قائل میشود. اثر هال، گواه این مطلب است که در فلزات، الکترونها، حاملهای بار هستند نه حفرهها.
ادامه بحث ولتاژ هال
اثر هال نشان داد که در بعضی مواد (به خصوص نیمههادی نوع p)، منطقیتر است فرض کنیم که حفرهها با بار مثبت در حال حرکت هستند نه بارهای منفی.
$$I_x=ntw(-v_x)(-e)$$
که در آن، n چگالی حاملهای بار، tw سطح مقطع جریان عبوری از هادی و −e بار الکترون است. با جایگزینی w در دو معادله بالا، ولتاژ هال به صورت زیر به دست میآید:
$$V_H=\frac{I_x B_z}{nte}$$
ضریب هال نیز به صورت زیر تعریف میشود:
$$R_H=\frac{E_y}{j_x B_z}$$
که در آن jx چگالی جریان حاملهای الکترون است.
$$j_x=\frac{I}{tw}$$
و Ey نیز میدان الکتریکی القایی است. پس داریم:
$$R_H=\frac{E_y}{j_x B}=\frac{V_H t}{IB}=-\frac{1}{ne}$$
از اثر هال میتوان برای اندازهگیری چگالی جریان یا میدان مغناطیسی استفاده کرد.
یکی از ویژگیهای مهم اثر هال، این است که بین بارهای مثبت عبوری در یک جهت و بارهای منفی عبوری در خلاف جهت تفاوت قائل میشود. اثر هال، گواه این مطلب است که در فلزات، الکترونها، حاملهای بار هستند نه حفرهها.
همچنین اثر هال نشان داد که در بعضی مواد (به خصوص نیمههادی نوع p)، منطقیتر است فرض کنیم که حفرهها با بار مثبت در حال حرکت هستند نه بارهای منفی.
اثر هال در نیمه هادیها
وقتی یک نیمههادیِ حامل جریان، در میدان مغناطیسی قرار گیرد، بر حاملهای جریان داخل نیمههادی، نیرویی وارد میشود. جهت این نیرو بر میدان مغناطیسی و بر جهت جریان عمود است. به این صورت، یک اختلاف ولتاژ در دو سر نیمههادی به وجود میآید.
فرمولهای اثر هال که در بالا بیان شد، وقتی صحت دارد که تنها یک حامل بار داشته باشیم. هرچند، در نیمههادیها، تئوری پیچیدهتر است. زیرا در این مواد، هدایت میتواند توسط الکترونها و حفرهها انجام شود. هرکدام از این حاملهای بار میتوانند چگالی و «قابلیت تحرک» (mobility) متفاوتی داشته باشند. برای میدانهای مغناطیسی محدود، ضریب هال به صورت زیر است:
$$R_H=\frac{p \mu_h^2 – n \mu_e^2}{e(p \mu_h^2 + n \mu_e^2)^2}$$
یا به طور معادل:
$$R_H=\frac{p-nb^2}{e(p+nb)^2}$$
که در آن:
$$b=\frac{\mu_e}{\mu_h}$$
در روابط بالا n، چگالی الکترونها، p چگالی حفرهها، قابلیت تحرک الکترونها، قابلیت تحرک حفرهها و e مقدار بار بنیادی است. برای میدانهای مغناطیسی بزرگتر، این رابطهها، با مدلی که تنها یک نوع حامل بار داریم، جایگزین میشود. این رابطهها را در بخشهای قبل بیان کردیم.
رابطه اثر هال با تولد ستاره
ثابت شده است که میدانهای مغناطیسی نقش مهمی در شکلگیری ستاره ایفا میکنند. تحقیقات نشان داده است که اثر هال در «رمبش گرانشی» (Gravitational Collapse) نقش دارد. این پدیده، دلیل ایجاد اولین ستارههاست.
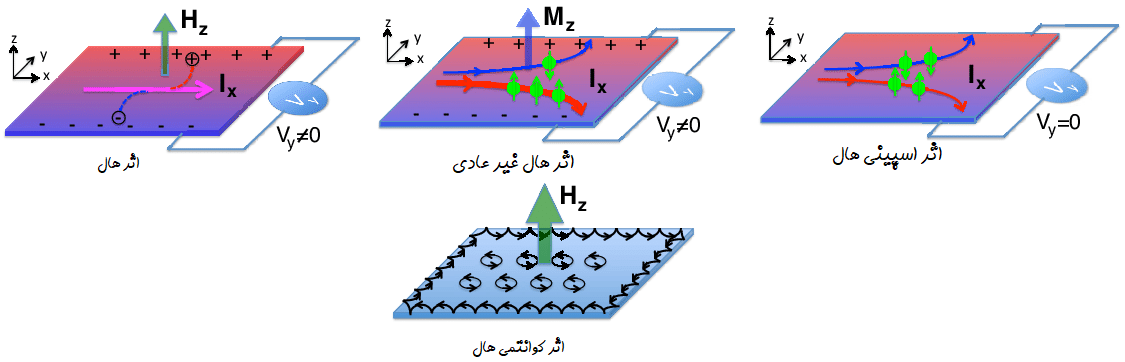
اثر اسپینی هال
پدیدهای است که توسط «دیاکونوف» و «پرل» در سال ۱۹۷۱ پیشبینی شد. در این حالت، هیچ احتیاجی به میدان مغناطیسی خارجی نیست. این میدان، توسط حرکت اسپینی الکترونها در اتمهای خودِ ماده، به وجود میآید.
اثر هال غیر عادی
این موضوع در مواد فرومغناطیس (یا مواد پارامغناطیس وقتی در معرض میدان مغناطیسی قرار میگیرند)، به صورت «اثر هال غیر عادی» (Anomalous Hall Effect) مشاهده میشود.این پدیده، به صورت مستقیم به خاصیت مغناطیسکنندگی ماده (M) مربوط است. معمولا این خاصیت از اثر هال معمول، بسیار بزرگتر است. مثلا در فلزی مانند نیکل در «دمای کوری»، ضریب هال غیر عادی، تقریبا صد برابر بزرگتر از ضریب هال معمول است. اما این دو ضریب در دماهای بسیار پایین تقریبا برابر هستند.
اثر کوانتومی هال
برای یک سیستم دو بعدی الکترون که با استفاده از ترانزیستور اثر میدان یا ماسفت قابل پیادهسازی است، در حضور میدان قوی مغناطیسی و دمای پایین، «اثر کوانتومی هال» (Quantum Hall effect) مشاهده شده است.
این سه پدیده در شکل زیر نشان داده شده است.
تصویر مورد استفاده، یکی از کاربردهای اثر هال یعنی «پیشرانه اثر هال» (Hall Effect Thruster) را نشان میدهد.
امیدواریم مطالب بالا مفید واقع گردد.ولیکن ما از اثر هال جهت قرائت جریان استفاده می کنیم . جهت آشنایی با این محصولات ما اینجا کلیک کنید .


